Source code from COMP302 course page. Some helper functions are not shown here.
This post is my attempt to understand the beauty and power of streams.
Intro
The stream type below allows finite and infinite streams. Finite streams end with an end-of-stream marker that is written as Eos. An infinite stream does not end so it will not have an end-of-stream marker.
type 'a stream = Eos | StrCons of 'a * (unit -> 'a stream)type 'a stream = Eos | StrCons of 'a * (unit -> 'a stream)To represent “infinity”, we need to **suspend ** the evaluation or no memory is large enough to hold infinite data. Here, we wrap the stream inside a function, and we “wake up” the stream by applying the function. We can never see the whole stream let alone print it, but we can ask for part of it, as long as this part is finite.
Examples
A stream of all ones
let rec ones = StrCons (1, fun () -> ones);;let rec ones = StrCons (1, fun () -> ones);;What is left after you take away the first 1 from infinitely many 1’s? Infinitely many 1’s!
So the code is saying: the stream starts with 1, and the rest of the stream also starts with 1, and the rest of the rest…
Natural numbers
let rec nums_from (n:int) = StrCons(n, fun () -> nums_from (n + 1));;
let naturals = nums_from 1 (* or 0 if you like *)let rec nums_from (n:int) = StrCons(n, fun () -> nums_from (n + 1));;
let naturals = nums_from 1 (* or 0 if you like *)Now we have 1,2,3,4,5…
Take out 1, we get an infinite stream starting from 2, then 3, then…
Fibonacci numbers
let fibs =
let rec fibgen (a: int) (b:int) =
StrCons (a, fun () -> fibgen b a+b )
in
fibgen 1 1let fibs =
let rec fibgen (a: int) (b:int) =
StrCons (a, fun () -> fibgen b a+b )
in
fibgen 1 1Below is a great picture that I found on stackoverflow for the famous one-liner in Haskell:
fib = 1 : 1 : (zipWith (+) fib (tail fib))fib = 1 : 1 : (zipWith (+) fib (tail fib))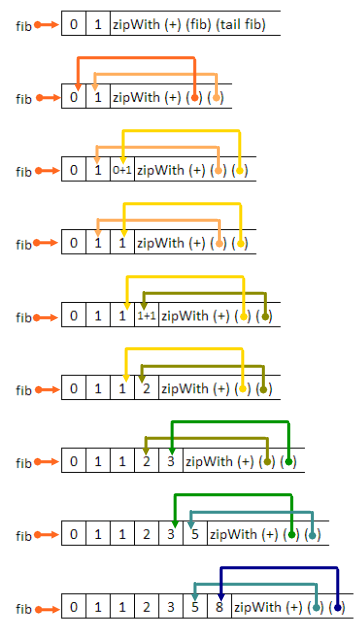
Partial sum
let rec partialsum (s: int stream) =
match s with
| Eos -> Eos
| StrCons (h, t) -> StrCons (h, fun () -> zipWith (+) (t()) partialsum s)
(*
* t() is necessary because t is fun() -> 'a stream
* We need to wake it up. It is taking the tail of the input stream
*)let rec partialsum (s: int stream) =
match s with
| Eos -> Eos
| StrCons (h, t) -> StrCons (h, fun () -> zipWith (+) (t()) partialsum s)
(*
* t() is necessary because t is fun() -> 'a stream
* We need to wake it up. It is taking the tail of the input stream
*)partialsum ones:
(* pseudocode *)
(* For convenience, I'll use shorthand for those functions *)
zw = zipWith (+) (a: 'a stream) (b: 'b stream)
ps = partialsum = [1, (zw [1,..] ps)]
(* Try to visualize this *)
ps = [1, (zw [1,..] ps)]
(* ps [1,1,..] =
* [1, 1+1, 1+2, 1+3 ]
* Translate it into human language:
* Take the next element in the input stream, add it to the last partial sum
* That is, ps[i] = input[i] + ps[i-1], where ps[i] is the i-th partial sum
*)
[ 1, (zw [1,..] ps) ]
[ 1, zw [1,..] ([1, (zw [1,..] ps)]) ]
[ 1, 1+1, zw [1,..] (zw [1,..] ps) ]
[ 1, 2, zw [1,..] (zw [1,..] [1, (zw [1,..] ps) ]]
[ 1, 2, zw [1,..] [2, (zw [1,..] (zw [1,..] ps) ]]
[ 1, 2, 3 zw ..]partialsum ones:
(* pseudocode *)
(* For convenience, I'll use shorthand for those functions *)
zw = zipWith (+) (a: 'a stream) (b: 'b stream)
ps = partialsum = [1, (zw [1,..] ps)]
(* Try to visualize this *)
ps = [1, (zw [1,..] ps)]
(* ps [1,1,..] =
* [1, 1+1, 1+2, 1+3 ]
* Translate it into human language:
* Take the next element in the input stream, add it to the last partial sum
* That is, ps[i] = input[i] + ps[i-1], where ps[i] is the i-th partial sum
*)
[ 1, (zw [1,..] ps) ]
[ 1, zw [1,..] ([1, (zw [1,..] ps)]) ]
[ 1, 1+1, zw [1,..] (zw [1,..] ps) ]
[ 1, 2, zw [1,..] (zw [1,..] [1, (zw [1,..] ps) ]]
[ 1, 2, zw [1,..] [2, (zw [1,..] (zw [1,..] ps) ]]
[ 1, 2, 3 zw ..]